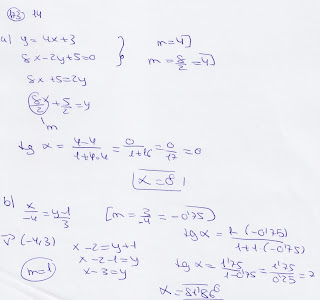Reflexión del examen

Mi reflexión sobre el examen de la anterior semana de matemáticas es, que me ha parecido que los problemas que nos ha puesto el profesor no eran excesivamente difíciles pero requieren mas practica en clase por que me surgieron dudas que no sabia como afrontarlas sin embargo como estamos en proceso de aprendizaje espero seguir aprendiendo y que en el siguiente examen no se me planteen las mismas dudas que me impidan resolver los problemas con facilidad y aprovecho a invitar a mis compañeros a que practiquemos entre nosotros y nos intercambiemos nuestras dudas y aprender unos de otros.

Operaciones con sucesiones

SUMA Y DIFERENCIA DE SUCESIONES:

La sua de dos sucesiones (an)y(bn) es otra sucesión(sn), que se obtiene al sumar los términos correspondientes de (an) y (bn).

 La diferencia de dos sucesiones (an) y (bn) es otra sucesión (dn), que se obtiene al restar a los términos de la primera los correspondientes de la segunda.






PRODUCTO DE UN NÚMERO REAL POR UNA SUCESIÓN:

El producto de un número real t por una sucesión(an) es otra sucesión (qn), que se obtiene al multiplicar por t cada término de (an).





PRODUCTO DE DOS SUCESIONES:

El producto de dos sucesiones (an) y (bn) es otra sucesión (Pn), que se obtiene al multiplicar los términos correspondientes de (an) y (bn).




COCIENTE DE SUCESIONES :

El cociente de dos sucesiones (an) y (bn) esta última con todos sus términos distintos de cero es otra sucesión(cn), que se obtiene al dividir los términos correspondientes de (an) y (bn).





Ejemplo : Ejercicios del tema 9 : 9 y 10

Sucesiones monótonas

SUCESIONES MONÓTONAS CRECIENTES :

Una sucesión (an) es monótona creciente cuando cada término es menor o igual que el término siguiente.



SUCESIONES ESTRICTAMENTE CRECIENTES :

Una sucesión (bn) es estrictamente creciente cuándo cada término es menor que el término siguiente.





SUCESIONES MONÓTONAS DECRECIENTES :

Una sucesión (cn) es monótona decreciente cuando cada término es menor o igual que el siguiente.




SUCESIONES ESTRICTAMENTE DECRECIENTES :

Una sucesión (dn) es estrictamente decreciente cuando cada término es mayor que el siguiente.

Ejemplo : Ejercicios del tema 9 : 7 y 8

Sucesiones acotadas

SUCESIONES ACOTADAS SUPERIORMENTE :

Una sucesión (an) está acotada superiormente por un número real K si todos los términos de la sucesión son menores o iguales que K.




a K se le llama cota superior de la sucesión
 

SUCESIONES ACOTADAS INFERIORMENTE :

Una sucesión (bn) está acotada inferiormente por un número real P si todos los términos de la sucesión
son mayores o iguales a P

A P se le llama cota inferior de la sucesión


SUCESIONES ACOTADAS :

Una sucesión (cn) está acotada si lo está superior e inferiormente.






 Ejemplo : Ejercicios del tema 9 del 4-6

Suceciones

Empezamos con ls sucesiones…

¿Qué es una sucesión?: una sucesión es una secuencia de números reales , ordenados uno detrás del otro.Cada uno de estos números se denomina término y se designan por:
a(1),a(2),a(3)…a(n)   o   a1,a2,a3…an
En los que el subíndice ocupa el término de la sucesión.
Al término an se le llama término general de la sucesión. 



Ejemplos: Ejercicios del tema 9 del 1-3

Elipse

Elipse: Es el lugar geometrico de todos los puntos P del plano que verifican que la suma de sus distancias a dos puntos fijos F y F´ llamados focos es una cantidad constante.





















Ejemplo: Halla los semejes la semidistancia focal y la excentricidad de la elipse 9x2+25y2=225

Hipérbola

Hipérbola: Es el lugar geométrico de los puntos P del plano que verifican que la diferencia de sus distancias a dos puntos fijos F y F´ llamados focos es cantidad constante K.

Ejemplo:    Halla la ecuación de una hipérbola con focos en F(0,2) y F´(0,-2) y de vértices en A(0,1) y A´(0,-1).

Cónicas: Mediatriz y Bisectriz

Mediatriz: Es la recta que pasa por el punto medio de un segmento y es perpendicular a ese segmento.

Ejemplo:














Bisectriz: Es la recta que pasa por el vértice del ángulo y lo divide en dos partes iguales.

-Para hallar las bisectrices igualamos las dos ecuaciones normales.








Ejemplo: Halla la bisectriz del ángulo C en el triángulo de vertices A(2,4) , B(1,1) y C(0,3)

Distancia entre dos puntos

                                  Fórmula

Ejemplo: Encontrar la distancia entre los puntos P(-2,4) y Q(3,4)

Distancia de un punto a una recta

                                         Fórmula:









 Ejemplo: Dado el punto P(2,-1) y la recta r, halla la distancia entre P y R

Ángulo que forman dos rectas

               Se llama ángulo que forman dos rectas al menor de los ángulos que definen

Ejemplo: Ejercicio14 página 173

Posiciones relativas de dos rectas en el plano

                                              DOS RECTAS EN EL PLANO PUEDEN SER:



-Secantes: si se cortan en un punto

-Paralelas: si no tienen ningún punto en común

-Coincidentes: si tienen todos sus puntos comunes




















Ejemplo: Ejercicio 12 pagina 172

Ecuaciones de la recta

                                    Distintas formas de expresar la ecuación de la recta

Ejemplo: página 172 ejercicio 9

geometria analítica (vectores)

Vector fijo: un vector fijo de origen a y extremo b , es un segmento orientado por :
-dirección o recta que lo contiene
-sentido u orientación de la recta
-módulo o longitud del segmento correspondiente

Coordenadas de un vector fijo : llamamos coordenadas de un vector fijo AB de origen A(a1,b1) y extremo B(a2,b2) a los números que se obtienen al restar a las coordenadas del extremo las del origen.







Módulo de un vector fijo: es la distancia entre el origen A(a1,b1) y el extremo B(a2,b2)












Ejemplo ejercicio 1 página 172 :









                                          Operaciones con  vectores :

    - SUMA:




    -RESTA:







  -PUNTO MEDIO

Producto  escalar : es un número y se define como :

propiedades:

Si dos vectores son perpendiculares su producto escalar es = 0

 Ejemplo ejercicio 3 pagina 172

Vector unitario: es aquel que su módulo vale 1

Ejemplo: ejercicio 6 página 172: