Examen de casa

Ejercicio 1

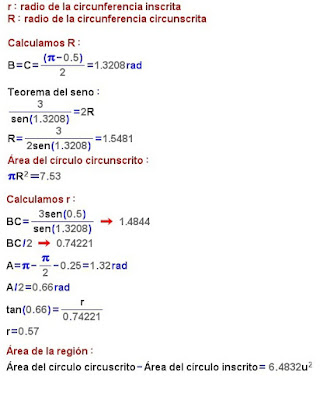
Definición de incentro de un triángulo. Calcula, paso a paso, utilizando WIRIS, el área de la región plana comprendida entre la circunferencia inscrita y la circunferencia circunscrita al triángulo isósceles cuyos lados iguales miden 3 unidades y el ángulo comprendido entre dichos lados mide 0’5 radianes. 

Ejercicio 2

Se quiere reconstruir la ubicación y las dimensiones de un claustro de forma cuadrada desaparecido y del que se ha encontrado su pozo. Se tienen dudas de la ubicación del pozo en relación al claustro pero se sabe que dicho pozo distaba 30, 40 y 50 m de las esquinas del claustro. Utiliza WIRIS para realizar los cálculos paso a paso y dibuja la solución con GEOGEBRA.

Ejercicio 3

Elabora una construcción dinámica con GEOGEBRA que permita ver dicha evolución después demuestra, utilizando el teorema de Tales, que el triángulo MPR es isósceles.Como el segmento AB se desliza por la semicircunferencia, el triángulo MPR varía, demuestra que cualquiera de esos triángulos MPR son semejantes.

Ejercicio 4

Resuelve el triángulo DEN sabiendo que ABCDE es un pentágono regular, M es el punto medio del radio, en el eje OX, de la circunferencia circunscrita a dicho pentágono y que tomamos como unidad de medida, N es un punto en el eje OX tal que DM = NM. Utiliza WIRIS para realizar los cálculos paso a paso y dibuja la figura con la solución utilizando GEOGEBRA.

Ejercicio página 131

Estos son los ejercicios que realizamos Laura y yo para prepararnos el examen y que nos han servido de gran ayuda. Ha sido una experiencia muy buena y que me gustaría repetir en la que he aprendido mucho de Laura y que también me ha servido para conocerla a ella,muchas gracias Laura:)

reflexion de los metrónomos

Si colocas 32 metrónomos sobre un objeto estático y rígido y los pones a funcionar desincronizados entre ellos, se quedarán así indefinidamente. Pero si los colocas sobre una superficie móvil, algo realmente interesante e hipnotizador sucede.

Los metrónomos de este vídeo son un ejemplo del segundo caso. La energía del movimiento de uno de los metrónomos afecta al movimiento de todos los demás metrónomos de su alrededor, mientras que la energía del movimiento de todos los demás metrónomos afecta al movimiento de nuestro metrónomo original. Toda esta comunicación ínter-metrónomo es facilitada por la tabla sobre la que descansan, que hace las funciones de intermediario energético entre todos los metrónomos colocados sobre ella. Los metrónomos de este vídeo (en realidad son sencillamente péndulos) están abocados a sincronizarse.

La matemática y la física detrás de la sincronización de metrónomos es de hecho relevante para gran variedad de fenómenos científicos, incluyendo la propagación del sonido y la conductividad térmica. 

Mi reflexión la enfoco en el trabajo en grupo : para que los trabajos en grupo puedan funcionar y conseguir los objetivos que se hayan establecido ,todos los miembros del grupo tienen la responsabilidad de llevar todas las actuaciones necesarias para que tanto su trabajo como el de sus compañeros de equipo salga bien y se consiga lo propuesto.

Sistemas de ecuaciones trigonométricas

                                                  Sistemas de ecuaciones trigonométricas

Ecuaciones trigonométricas

                                                      Ecuaciones trigonométricas       

Transformaciones de sumas de dos razones en producto

Razones trigonométricas del ángulo mitad

                                      Razones trigonométricas del ángulo mitad  
OBTENEMOS LAS RAZONES TRIGONOMÉTRICAS DEL ÁNGULO MITAD a/2 A PARTIR DEL COSENO DEL ÁNGULO DOBLE

EJEMPLO:

Razones trigonométricas del ángulo doble

                                                 Razones trigonométricas del ángulo doble
OBTENEMOS FACILMENTE LAS RAZONES TRIGONOMÉTRICAS DEL ANGULO DOBLE 2a, A PARTIR DE LAS RAZONES TRIGONOMÉTRICAS DE LA SUMA DE DOS ÁNGULOS

Teoremas de adicción

                                                              Teoremas de adicción     

Ejercicios

Ejercicio 22

                                                                   Ejercicio 22

Teorema del seno y area de un triángulo

                                                 Teorema del seno y area de un triángulo

teorema del coseno

                                                     teorema del seno                                                            

ej 11 pag 108

Relacciones fundamentales

ortocentro, baricentro, circuncentro, incentro,

Ortocentro

Es el punto de corte de las tres alturas.

Baricentro

Es el punto de corte de las tres medianas.

Circuncentro

Es el punto de corte de las tres mediatrices.

Incentro

Es el punto de corte de las tres bisetrices.

demostración de los ángulos 30º,45º,60º

ejercicio de las razones trigonométricas

tema 4 :trigonometria

ej 40 y 44

ej 40

ej 44

Ejercicios del examen : 22 y 48

ej 48

                                  ej 22

Ecuaciones polinómicas

Esta ecuación ax+b=0 se resuelve en el video anterior y nos muestra 3 soluciones que son:


1ºCompatible determinada si a es diferente de 0 la solución será un numero entero
2ºCompatible indeterminada cuando a=0 y b=0 la solución son todos los números reales infinitos
3ºIncompatible cuando a=0 y b es distinto de 0 la solución es que no hay ningún valor de x que cumpla la igualdad.

Tema 3 ecuaciones

Identidad de Sophie Germain

SOPHIE GERMAIN

Sophie Germain

BIOGRAFIA
Marie-Sophie Germain ( 1 de abril de 1776 – 27 de junio de 1831) fue una matematica francesa que hizo importantes contribuciones a la teoría de números y la teoría de la elasticidad. Uno de los más importantes fue el estudio de los que posteriormente fueron nombrados como números primos de SophieSus padres se opusieron a que estudiara matemáticas hasta que no tuvieron opción y lo aceptaron. Germain no podia ir a la escuela porque no aceptaban mujeres; pero se las arreglaba para recibir apuntes de los profesores. A ella le atrajo el análisis de Lagrange y bajo un nombre ficticio le escribió una composición. A éste le impresionó tanto, que averiguó quien era y fué a su casa a decirle lo impresionado que estaba. Esto le dio a Germain ánimo para tener el coraje de seguir estudiando matemáticas. Como resultado de un libro escrito por Gauss, Germain le escribió usando el mismo pseudónimo que habia usado con Lagrange. Gauss se interesó tanto en sus observaciones, que mantuvieron correspondencia por varios años. En 1807, Gauss se enteró del verdadero nombre de Germain. Ella temía que a Gauss le sucediera algo y envió unas tropas a la casa de él para asegurarse de que estuviera bíen. Cuando los soldados le hablaron de Germain, él les dijo que no la conocia. Luego, por cartas se esclareció la situación.Germain trabajó en el problema de la ley matemática de vibraciones de superficies elásticas. En 1811 sometió un trabajo al respecto a la Academia Francesa de las Ciencias (anónimamente); pero fue criticada por la falta de precisión al pasar de una linea a una superficie. En 1813 sometió otro trabajo del mismo tema y en 1816 ganó el primer lugar situándola entre los mejores matemáticos. Esto hizo que la aceptaran entre los círculos de matemáticos. Continuó escribiendo sobre distintos problemas malemáticos y continuó intercambiando correspondencia con Gauss. Este pidió a la Universidad de Göttingen que le dieran el grado de doctora; pero el 26 de junio de 1831 murió, antes de poder recibir el grado.


SUS DESCUBRIMIENTOS FUERON :

 La teoría de números fue la demostración matemática de la siguiente proposición: si x, y, z son enteros y x5 + y5 = z5, entonces al menos uno de ellos (x, y, o z) es divisible por cinco. Esta demostración, que fue descrita por primera vez en una carta a Gauss, tenía una importancia significativa ya que restringía de forma considerable las soluciones del último teorema de Fermat, el famoso enunciado que no pudo ser demostrado por completo hasta 1995.
Una de sus más famosas identidades, más comúmente conocida como Identidad de Sophie Germain expresa para dos números x e y que:

Sus primeros trabajos en Teoría de Números los conocemos a través de su correspondencia con Gauss. Entre 1804 y 1809 Sophie escribió a Gauss una decena de cartas en las que le comentaba sus investigaciones. Las primeras estaban firmadas con el pseudónimo Le Blanc. En 1819 se reanudó esta correspondencia.En 1808 comunicó a Gauss su más brillante descubrimiento en Teoría de Números. Demostraba que si x, y, z son números enteros, tales que x 5 +y 5 +z 5 =0 entonces, al menos uno de los números x, y o z debe ser divisible por 5. Más tarde generalizó este resultado en el teorema que hoy lleva su nombre.

Proposición de raíces racionales de un polinomio con coeficientes enteros

Ejemplos de fracciones algebraicas

Fracciones algebraicas

Una fracción algebraica es el cociente de dos polinomios y se representa por: 

P(x) es el numerador.

Q(x) es el denominador.

Fracciones algebraicas equivalentes

Dos fracciones algebraicas

son equivalentes, y lo representamos por:

si se verifica que P(x) · S(x) = Q(x) · R(x).

Ejemplo 

son equivalentes porque:

(x+2) · (x− 2) = x² − 4

Dada una fracción algebraica, si multiplicamos el numerador y el denominador de dicha fracciónpor un mismo polinomio distinto de cero, la fracción algebraica resultante es equivalente a la dada.

Simplificación de fracciones algebraicas

Para simplificar una fracción algebraica se divide el numerador y el denominador de la fracción por un polinomio que sea factor común de ambos.

Ejemplo 

Amplificación de fracciones algebraicas

Para amplificar una fracción algebraica se multiplica elnumerador y el denominador de la fracción por un polinomio. 

Ejemplo